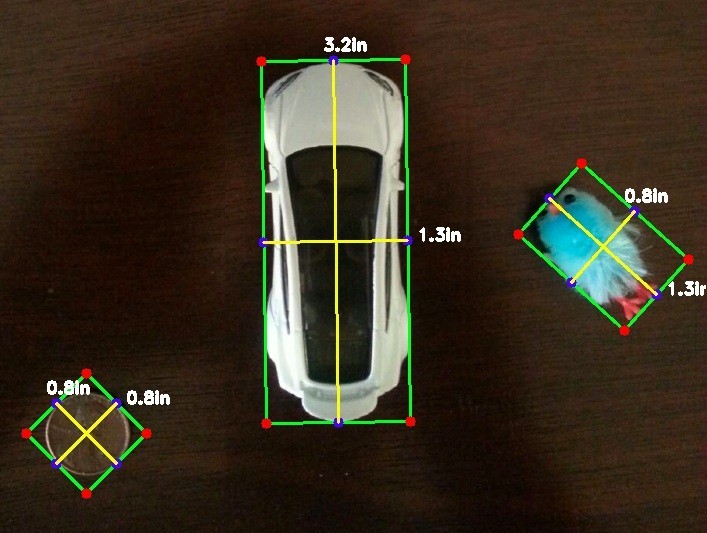
Calculating the Size of Objects in Photos with Computer Vision
Table of Contents Overview Setup Windows Linux OSX OpenCV Basics Getting Started Takeaways Overview You might have wondered how it is that your favorite social

Table of Contents Overview Setup Windows Linux OSX OpenCV Basics Getting Started Takeaways Overview You might have wondered how it is that your favorite social
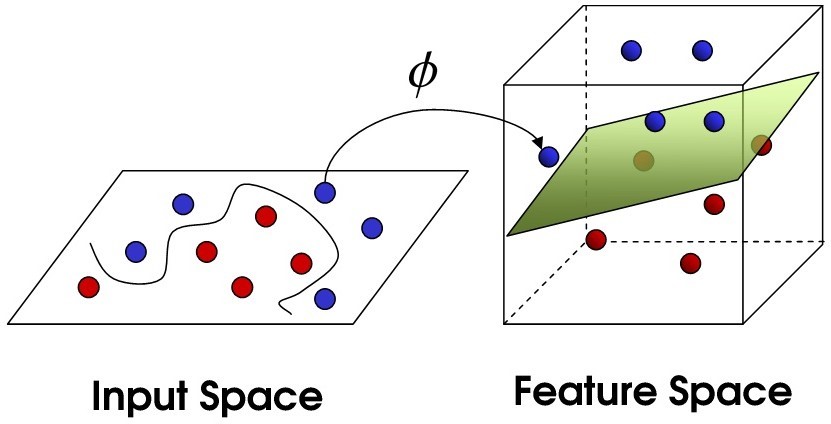
Table of Contents Overview Support Vector Machines (SVM) The Data Setup and Installation Exploring and Modeling the Data Takeaways Overview The object of this tutorial



Get personalized expert advice within two hours.