Table of Contents
ToggleHash table is a data structure designed for quick look ups and insertions. On average, its complexity is O(1) or constant time. The main component of a hash table is its hash function. The better the hash function, the more accurate and faster the hash table is. High level process of implementing a hash table is as follows: data is sent to a hash function where it gets evaluated and assigned an index number in an array. The hashing algorithm stores the data under the designated index with a pointer. When a lookup is requested for the same data, the algorithm sends the data to the same hash function and retrieves the index of the data in constant time.
A hash table which is also known as hash map, dictionary or just map is a data structure that arranges data for quickly looking up values with a given key.
Average run time complexity of a hash table is O(1) or constant time.
Hash tables are very similar to arrays. Arrays store values in sequential order and they have indices that can be used to look up values instantly. However, arrays have several restrictions: First of all, the indices are generated by the computer in sequential order. Second, if we want to add a value at the beginning or in the middle of the array, we need to move the rest of the values, which requires O(n) steps in the worst case scenario. And in some cases, when we are using non-dynamic arrays, their sizes are fixed.
Hash tables are like giving super powers to arrays. First, instead of relying on sequential indices, we use a function that turns keys into indices. That function is known as the hash function. Hash function is a special function that takes in a key and spits out an index. There are different ways of making hash function and we will look into them later. So then we store the values under that specific index. Later we can use the same function to get the indices and look up values in constant time just like with arrays.
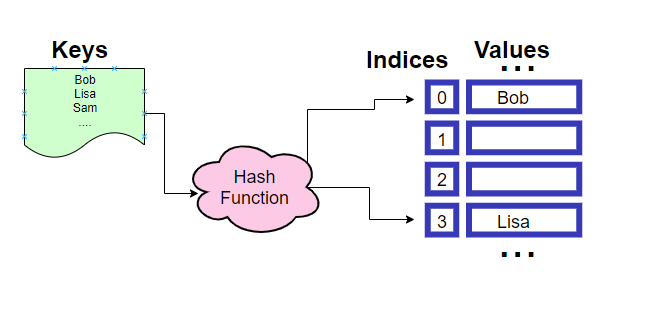
Example
Let’s look at an example case where using a hash table would be a good fit. Let’s say there is a list of students at a university with basic information. |Name|Major|Year| |-|-|-| |Bob|Math|2| |Sam|Biology|1| |Lisa|Art|3|
Now we are asked to organize this data for quick look ups and insertions. Using a hash table we can easily accomplish this task. First we have to pick a key from the list to identify each record. Typically, it is required to choose some value that is unique for each element. But for simplicity purposes we just pick the student names. So we have an array with 5 slots or buckets. Instead of assigning each record in order, we use a hash function to determine which slot each record goes to. We take Bob and give it to the hash function hash('Bob') and the function returns us an index value of 0, for example. We store Bob’s details under the index 0. Then we send Sam to the hash function, the functions tells us to store Sam’s details in slot 4. We do the same for Lisa and store her information in bucket 3.
Hash Function
Now let’s discuss what happens in our hash function. There are countless ways of making hash functions. It is usually preferred to use the ones on the internet which were tested by many people. However, for the sake of understanding the details under the hood, we can implement a simple one here.
Hash function logic We take ASCII value of each character and add them up.
| Total | %5 | ||||
|---|---|---|---|---|---|
| B | o | b | |||
| 66 | 111 | 98 | 275 | 0 | |
| S | a | m | |||
| 83 | 97 | 109 | 289 | 4 | |
| L | i | s | a | ||
| 76 | 105 | 115 | 97 | 393 | 3 |
For example, for Bob the sum of ASCII values would be 275. Since we have only 5 slots in our array we have to reduce the number to a smaller one. We can use a modulo operator to do that. 275 % 5 = 0
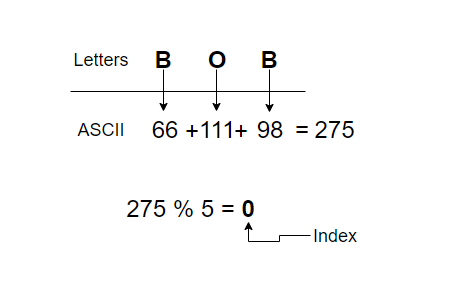
That means we store Bob’s details in slot 0.
Collisions
Remember we said the run time complexity of a hash table is constant – O(1) earlier? Well, its not entirely true. In the worst case scenario, complexity can be as bad as O(n). Main reason for that is the collisions. Collision is a situation when hash function outputs a duplicate index number.
For example, if we send the name Mia to our previous hashing function, it returns index 4. However, that slot is already occupied.
So there are 2 common ways of handling this issue. First one is called Linear Probing. With linear probing, we look at the given index, and if its occupied we go to the next available slot. In our example, there is no next slot. So in this case, we have to wrap around. Meaning we start from the beginning looking for an empty spot. 0 is also taken. We move to slot 1. That place is empty. We insert Mia at index 1. We keep repeating this process for other values if any collisions occur.
Second method is called Chaining. Here we use Linked list to handle duplicate index issues. If you don’t know what a linked list is, here is a good source to read about it. For this method to work, the hash table needs to be properly implemented. All slots should be pointing to the head of the linked list. Then when there is a collision we store the value in the next chain of the linked list. During look ups we need to ensure to check for all nodes by iterating through the list. That is why run time complexity sometimes can be a O(n)
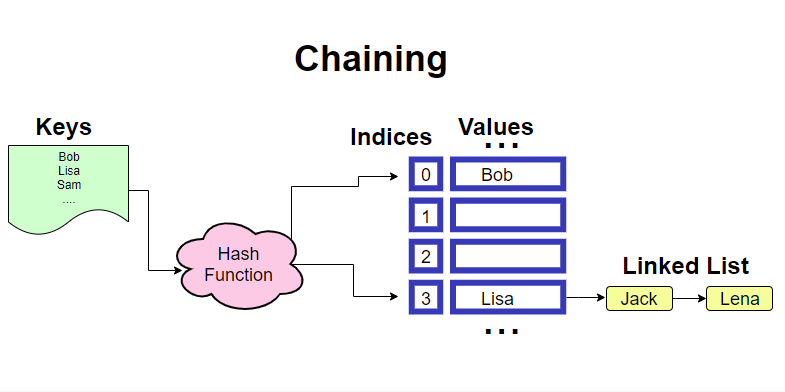
Hash Table in JavaScript
In JavaScript hash table is called Object.
const hash_map = {
'key':'value'
};Values in objects could be any type: string, array, integer or even another object. For example, to create an object for the data we had earlier we do the following
const map = {
Bob: {
name: 'Bob',
major:'Math',
year: 2,
},
Sam: {
name: 'Sam',
major:'Biology',
year: 1,
}
};Insertion
If we want to insert new key value pairs in the object, we can do it in two ways. First we can use dot method. Second way is similar to **array look up
map['Lisa'] = {
name: 'Lisa',
major':'Art',
year: 3,
};
// OR
map.Lisa = {
name: 'Lisa',
major':'Art',
year: 3,
};Removal
delete map.Bob;
// OR
delete map['Bob']Update
map.Lisa.year = 4;
// Or
map['Lisa']['year'] = 4;Look up
console.log(map.Sam.major);
// Output: 'Biology'
// OR
console.log(map['Sam']['major']);
// Output: 'Biology'Cheers









