What’s All the Fuss About Features? Features are interesting aspects or attributes of a thing. When we read a feature story, it’s what the news
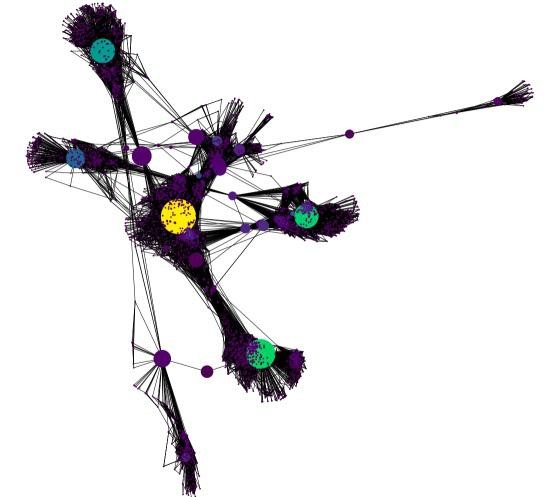
Graphs, Graph theory, Euler, and Dijkstra As tasks become more defined, the structures of data used to define them increase in complexity. Even the smallest
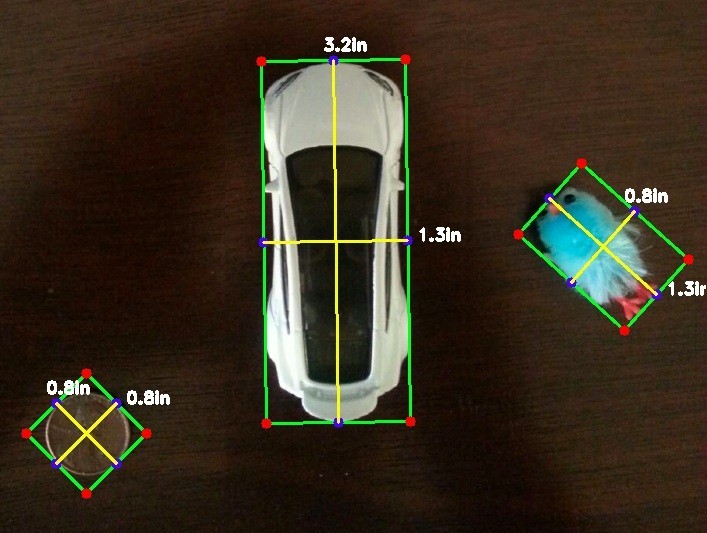
Table of Contents Overview Setup Windows Linux OSX OpenCV Basics Getting Started Takeaways Overview You might have wondered how it is that your favorite social
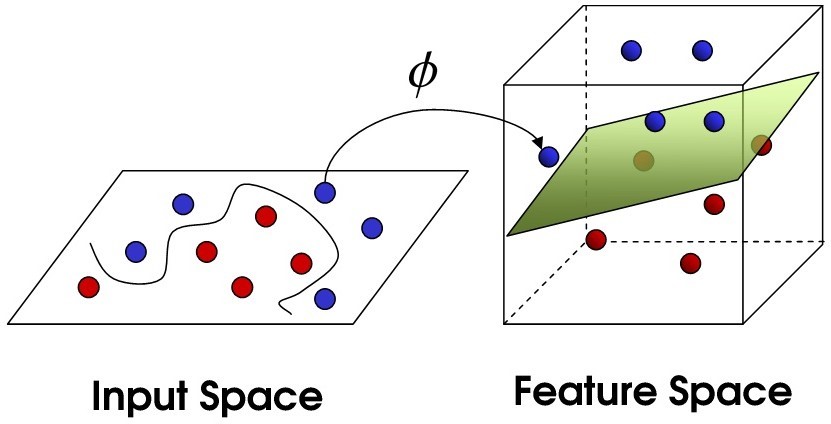
Table of Contents Overview Support Vector Machines (SVM) The Data Setup and Installation Exploring and Modeling the Data Takeaways Overview The object of this tutorial
Get personalized expert advice within two hours.
