Table of Contents
ToggleWhether we know it or not, trees are everywhere: our computer file systems, HTML DOM, XML/Markup parsers, PDF format, computer chess games, compilers, and others heavily rely on the tree data structure. More practical examples are company hierarchies, family trees, or comments section of any posts. Trees are found to be tricky when implementing in applications and during the coding interviews. How about we take a deep dive in the details of trees and learn the concepts in a more straightforward and fun way? In this article, we look at different types of trees and build a few of them from scratch to solidify our knowledge. Also, we use lots of visuals, which is the key to remembering. Let’s get started!
Outline
- What is a tree?
- Terminology
- Implementation of a general tree
- Traversing a general tree
- Binary trees
- Binary tree traversal
What is a tree?
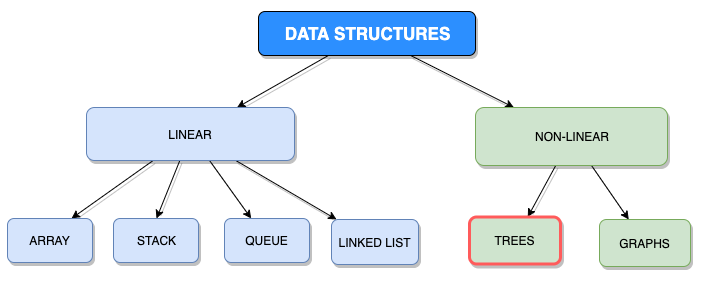
A tree is a non-linear data structure composed of nodes. It organizes values hierarchically. A node is an entry in a tree, and every node can have zero or more child nodes.
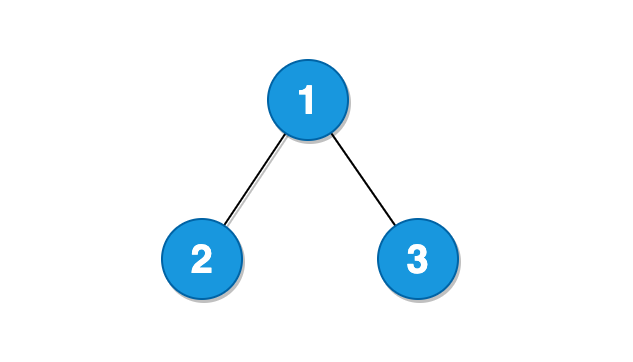
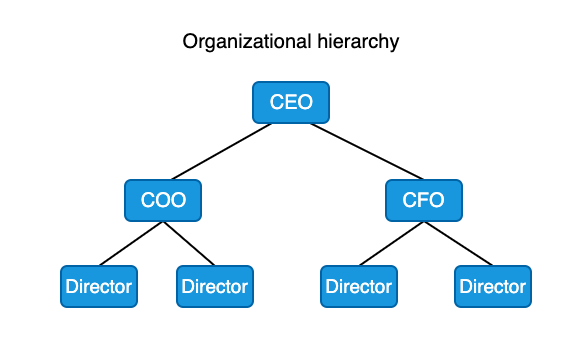
A typical company structure is an excellent example of a hierarchy. There is always a root node at the top of the tree (It looks like a tree when it is flipped upside down) and nodes are connected by edges.
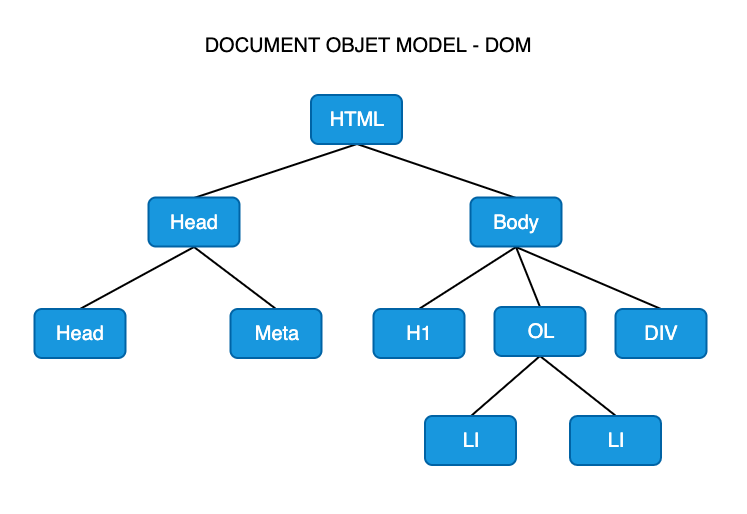
Another example of a hierarchy is the HTML DOM (Document Object Module).
Terminology
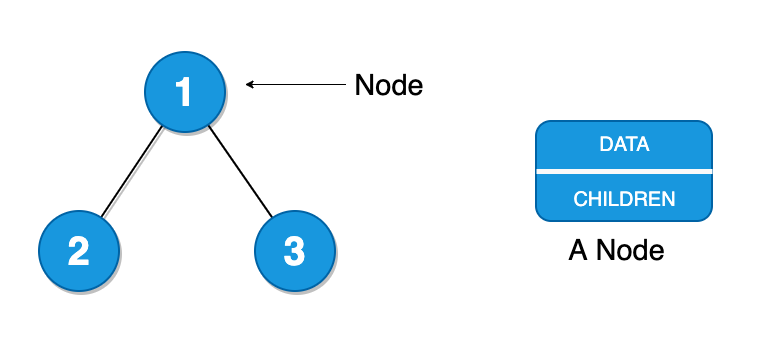
– Node
A node is an entry in a tree. It can contain any type of data. It may or may not have child nodes.
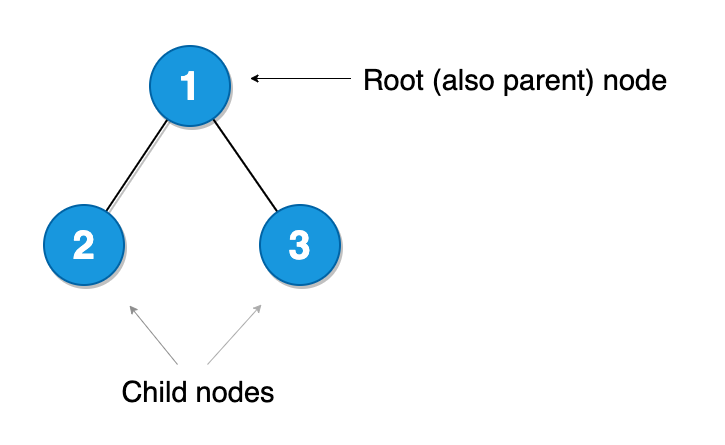
– Root node
Root node is also a parent node to its children.
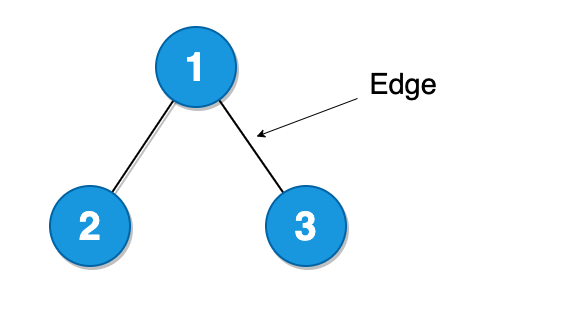
– Edges
Nodes are connected by edges.
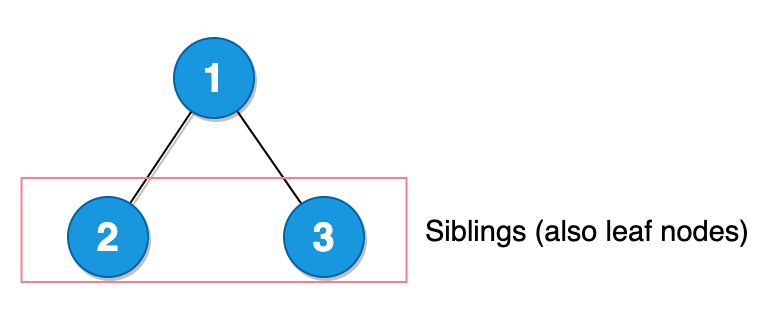
– Siblings
Siblings are the child nodes of the same parent.
– Leaf
A leaf node is a node that does not have any child nodes in the tree.
– Depth (or Level)
The number of links or edges from the root node to a selected node is called the depth of the selected node.
– Height
Height of a tree is equal to the maximum depth, or the number of edges from the root to the furthest leaf.
General Tree Implementation
Trees are usually built-in with most of the programming languages. However, to understand it better, we can build one from scratch. Let’s use JavaScript to implement it.
First, we create the Node class that contains the necessary methods to manage the tree.
class Node {
constructor(data){
this.data = data;
this.children = [];
}
add(data){
this.children.push(new Node(data));
}
remove(data){
this.children = this.children.filter(node => node.data !== data);
}
}Then we make the Tree class that can use the Node class to create nodes.
class Tree {
constructor(){
this.root = null;
}
}We utilize both to create and manage a general tree.
const node = new Node(44);
const tree = new Tree();
tree.root = node;Traversing A General Tree
There are two major algorithms that we can use to traverse a general tree – Breadth-First and Depth-First.
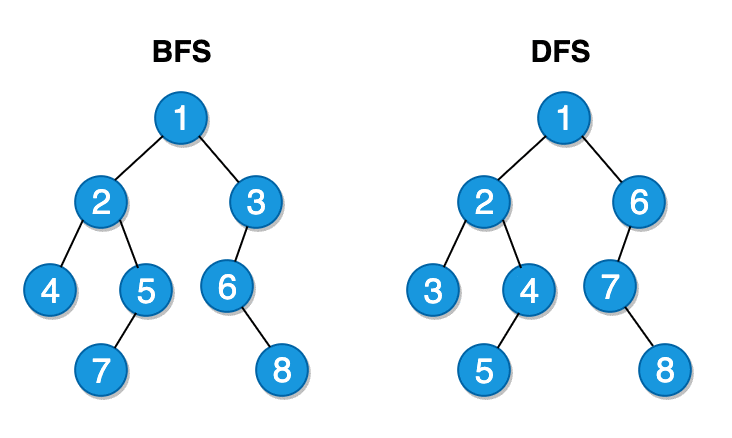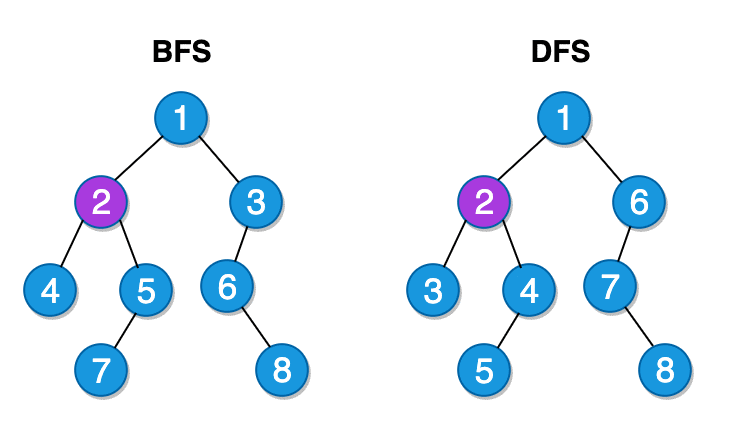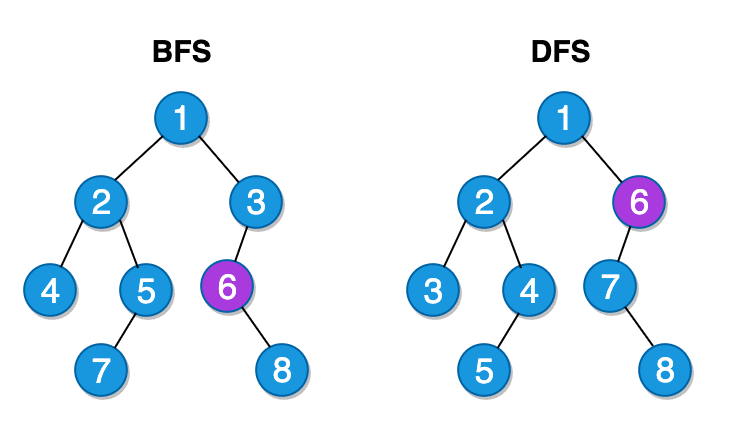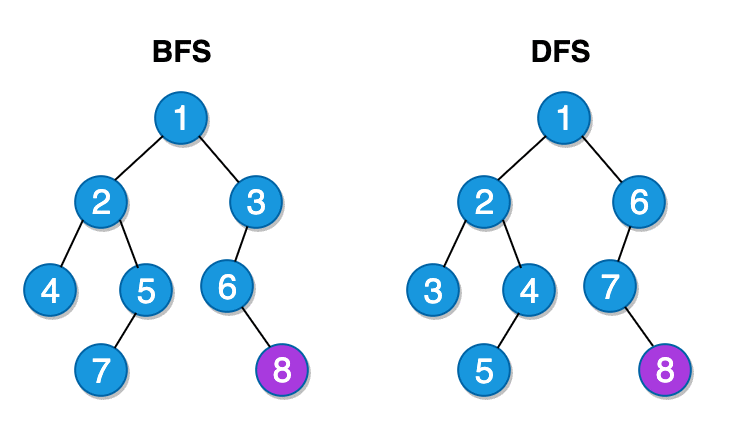
Breadth-First Traversal (BFS)
Breadth-First method tries to stay as close to the root node as possible. Once it starts going through the nodes, it traverses siblings nodes in a row until it reaches that last row.
Depth-First Traversal (DFS)
In DFS, we explore each branch until the end, before moving on to the next branch. It believes in going all the way down to the leaf nodes.
In order to check if a value exists in a tree, we could use either of these algorithms. Let us add these methods to the Tree class we have created earlier and see it in action.
class Tree {
constructor(){
this.root = null;
}
// Breadth-First Search
searchBF(value){
const queue = [this.root];
while(queue.length){
const node = queue.shift();
if(node.data === value){
return true;
} else {
queue.push(...node.children);
}
}
return false;
}
}Breadth-First method first creates a queue with the root element of the tree. It then utilizes a while loop as long as the queue is not empty. When it is empty, it stops. Inside the while loop, it removes the first element and assigns it to a variable. If the removed node contains the value we are looking for, it returns true confirming that the value exists in the tree. Otherwise, it just pushes the children of the removed node to the back of the queue and keeps doing this process until the queue is empty or the value is found.
class Tree {
constructor(){
this.root = null;
}
// Depth-First Search
searchDF(value){
const stack = [this.root];
while(stack.length){
const node = stack.shift();
if(node.data === value){
return true;
} else {
stack.unshift(...node.children);
}
}
return false;
}
}Depth-First method is very similar to the BFS. There is only one small difference. With non-recursive implementations, we use a stack to keep track of the nodes while exploring them instead of a queue. So instead of pushing the child nodes to the back of the array, we unshift them at the front.
Checkout the documentations for shift and unshift, if you are not familiar with them.
DFS and BFS are also commonly used on Graphs
Both of the methods perform the same task – traverse through a tree. It depends on the situation when to use which. Here are some points about the two approaches that can assist in determining the best option.
DFS and BFS Comparison
- DFS is usually preferred in order to explore all the nodes of a graph
- BFS is often better at finding the shortest path between two nodes
- BFS is implemented using queues and DFS is implemented using stacks
- BFS and DFS can also be built with recursion
Binary Trees
A binary tree is a very commonly used type of tree that has one distinctive feature – each node in a binary tree can have at most two children.
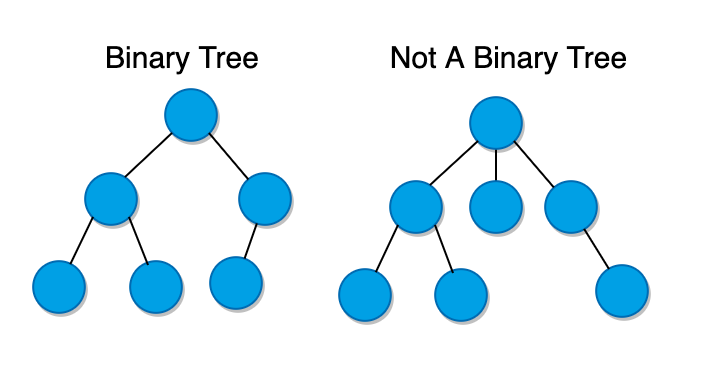
Also, there are different types of binary trees that we need to be aware of.
1. Balanced & Unbalanced Binary Trees
A balanced binary tree is a tree that has a “filled look” and can ensure O(log n)O(logn) times for insertion and search. It does not have to have a perfectly equal number of nodes on each side. It just should not have really short branches or missing pieces.
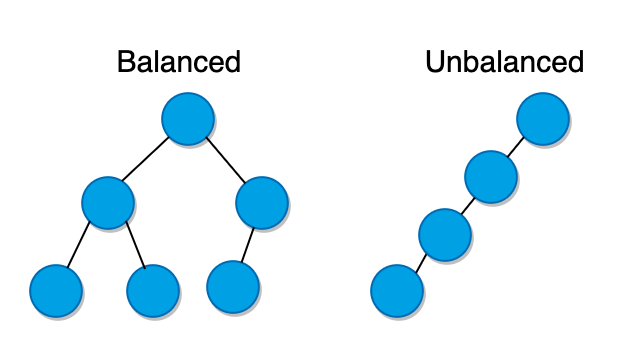
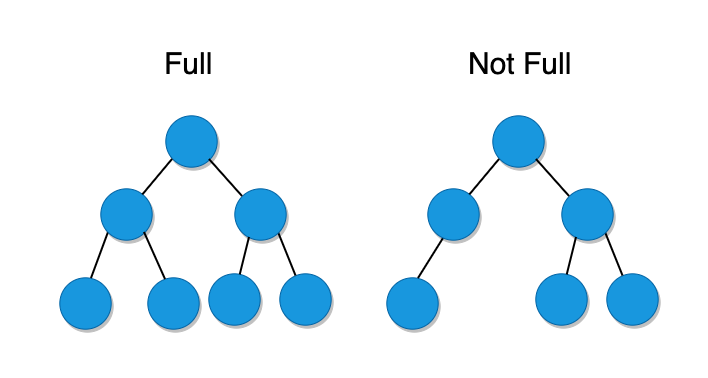
2. Full Binary Trees
If every single node in a tree has either two or zero children, we can call it a full binary tree. There cannot be a node with only one child in a full binary tree.
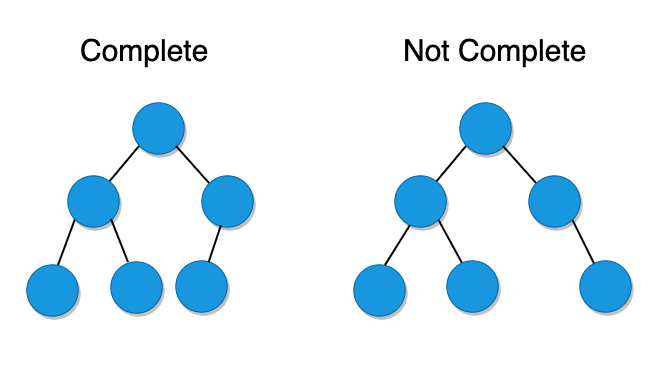
3. Complete Binary Trees
A complete binary tree needs to have almost all levels fully filled from left to right. Only the last level might be unfilled.
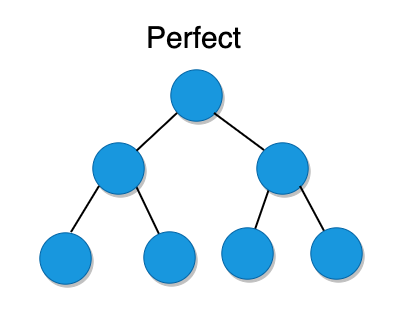
4. Perfect Binary Trees
Perfect binary trees are the ones that are complete and full. There must be exactly 2^k – 12k−1 nodes in a perfect binary tree (where kk is the depth of the tree).
Binary Tree Traversal
There are three main methods of traversing binary trees: Pre-Order, In-Order and Post-Order traversal.
Pre-Order Traversal
Pre-order traversal visits the current node, then explores the left subtree, then right subtree. In this type of traversal, the root node is always the first node visited.
class Node {
constructor(data){
this.data = data;
this.right = null;
this.left = null;
}
}class Tree {
constructor(){
this.root = null;
}
preOrder(node){
if(node !== null){
console.log(node.data);
this.preOrder(node.left);
this.preOrder(node.right);
}
}
}In-Order Traversal
With this method, we visit the left branch, then the current node and then the right branch nodes.
inOrder(node){
if(node !== null){
this.preOrder(node.left);
console.log(node.data);
this.preOrder(node.right);
}
}Post-Order Traversal
This method explores the node’s children first, left subtree, right subtree, and then the current node itself.
postOrder(node){
if(node !== null){
this.preOrder(node.left);
this.preOrder(node.right);
console.log(node.data);
}
}Summary
A tree is a common non-linear data structure that is a part of the applications and devices we use on a daily basis. It can be an extremely efficient way of organizing data when implemented correctly. Furthermore, trees are often discussed in coding interviews, and interviewees find it to be challenging to utilize. In this article, we simplify the tree data structure by looking at it from a high level and getting into details to demystify the tricky concepts.
NEXT: Tree Data Structure Simplified – Part 2