Table of Contents
ToggleWe use Google search, google maps, and social networks regularly nowadays. One of the things they all have in common is the fact they use a remarkable data structure – graphs under the hood to organize and manipulate data. You may have seen this data structure in college but don’t remember much about it. Or maybe it is a scary topic you avoid all the time. Either way, now is an excellent time to get familiar with it. In this blog, we will cover most of the concepts, and you should be comfortable to move on to work with algorithms related to graphs.
Outline
- Definition
- Terminology
- Representations
- Graph algorithms
Definition
A graph is a non-linear data structure that organizes data in an interconnected network. It is very similar to trees. Actually, a tree is a connected graph with no cycles. We will talk about the cycles in a little.

Ignore the red stroke around the Trees box. It was supposed to be around the Graphs box. ?

Random graph
There are two primary components of any graph: Nodes and Edges.

Nodes are typically called Vertices (singular: vertex), and they can represent any data: integers, strings, people, locations, buildings, etc.

Edges are the lines that connect the nodes. They can represent roads, routes, cables, friendships, etc.

Graph Terminology
There is a lot of vocabulary to remember related to graphs. We will list the most common ones.
Undirected and Directed graphs
A graph can be directed or undirected. As you might have already guessed, directed graphs have edges that point to specific directions. Undirected graphs simply connect the nodes to each other, and there is no notion of direction or whatsoever.

Weighted and Unweighted graphs
Let’s say we are using a navigation application and trying to get the best route between point A and point B. Once we enter the details of the two points, the app does some calculations and shows us the fastest way to reach our goal. Typically, there are many ways to get from point A to point B. So to choose the best way, the app would need to differentiate the options by specific values. The obvious solution, in this case, is to calculate the distance each option entails and pick the one with the shortest distance. So assigning some value to the connection between two points is called adding weight to it. Weighted graphs have some values (distance, cost, time, etc.) attached to their edges.
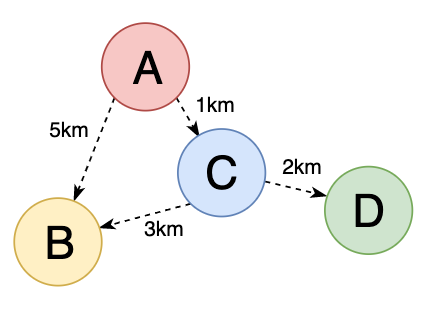
Cyclic and Acyclic graphs
Earlier, we have mentioned that a tree is actually a graph without cycles. So what is a cycle in a graph? We say a graph is cyclic when it has a continuous sequence of vertices that connects back to itself. Vertices or edges cannot be repeated. Acyclic graphs do not have cycles. Trees happen to be acyclic and directed graphs with a restriction that a child node can have only one parent node.

Representing graphs in memory
One of the main things that make graphs less intuitive and confusing is probably the way they are stored in computer memory. With the nodes being all over the place and flexible amounts of edges connecting them together, it can be challenging to find an obvious way to implement them. However, there are some widely accepted representations we can consider. Let’s store the following undirected graph in three different ways.
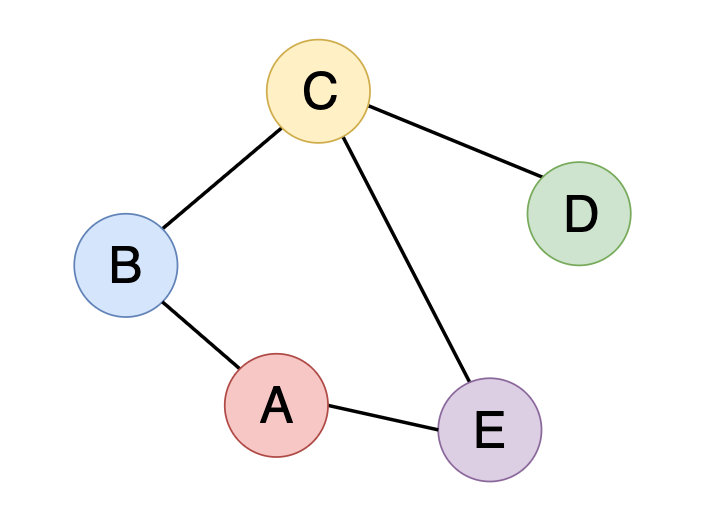
Edge List
This representation stores a graph as a list of edges.
const graph = [['A', 'B'], ['A', 'E'], ['C', 'B'], ['C', 'E'], ['C', 'D']];
Edges are mentioned only once on the list. There is no need to state A and B, and also B and A. Additionally, the order of edges in the list does not matter.
Similar to the list of edges, we could also store the nodes as a list. But that is not what the Edge List representation is.
Adjacency List
This method relies on the indexes when storing the connections to a particular node. In JavaScript, we would create an array of arrays, where each index indicates a node in the graph, and value at each index represents the adjacent (neighbor) nodes.
const graph = [
['B', 'E'],
['A', 'C'],
['B', 'D', 'E'],
['C'],
['A', 'C']
]
Again, the order of the nodes does not really matter, as long as we organize them without duplicates and with correct adjacent vertices.
Moreover, the graph could also be represented as an object. In that case, keys would represent the nodes and values would be the list of neighbor nodes:
const graph = {
'A': ['B', 'E'],
'B': ['A', 'C'],
'C': ['B', 'D', 'E'],
'D': ['C'],
'E': ['A', 'C']
}
This option is usually helpful when the vertices do not properly map to array indexes.
Adjecency matrix
In this representation, we create an array of arrays in which each index indicates a node, and value at that node shows the list of nodes this particular node has connections with. A connection is denoted as 1, and a lack of connection is denoted as 0.
const graph = [
[0, 1, 0, 0, 1],
[1, 0, 1, 0, 1],
[0, 1, 0, 1, 1],
[0, 0, 1, 0, 0],
[1, 0, 1, 0, 0]
]
In this case, the order of the nodes in the list matters.

Graph Algorithms
BFS and DFS
There are two main graph algorithms that we absolutely need to know when it comes to graphs:
- Breadth-First Search
- Depth First Search
Many graph-related problems can be solved with these two traversal methods.
Breadth-First Traversal
BFS algorithm traverses a graph by visiting the neighbor nodes instead of going down to the child nodes. And it uses a queue data structure to keep track of the visited vertices.

The structure given above looks like a tree, but it does not have to be a tree data structure for us to use the breadth-first search algorithm. Actually, a tree is a type of graph.
There are three main steps that these algorithms follows:
- Visit the adjacent unvisited node. Mark it as a visited node by pushing it in a queue.
- If no neighbor vertex is found, pop the first node from the queue and use it as the new starting point for a search.
- Repeat the steps above until there is nothing left in the queue
Depth-First Traversal
This algorithm visits the child vertices before traversing the sibling nodes. It tries to go as deep as possible before starting a new search on the graph. The significant difference of this algorithm from the previous breadth-first is the fact that it uses stack data structure instead of a queue.

DFS follows these steps to traverse through a graph:
- Visit the unvisited neighbor node. Push it in a stack. Keep doing it until there is no adjacent node is found.
- If no adjoining node is found, pop the first node from the stack and use it as the next starting point
- Repeat the steps above until the stack is clear
Cheers!